24. Applications of Taylor Series

Start with the series: \[ \ln(1-t) =\sum_{n=1}^\infty \dfrac{-t^n}{n} =-\,t-\dfrac{t^2}{2}-\dfrac{t^3}{3}-\dfrac{t^4}{4}-\cdots \] Divide by \(t\): \[ \dfrac{\ln(1-t)}{t} =\sum_{n=1}^\infty \dfrac{-t^{n-1}}{n} =-1-\dfrac{t}{2}-\dfrac{t^2}{3}-\dfrac{t^3}{4}-\cdots \] And integrate: \[\begin{aligned} \int_0^x \dfrac{\ln(1-t)}{t}\,dt &=\left[\sum_{n=1}^\infty \dfrac{-t^n}{n^2}\right]_0^x =\sum_{n=1}^\infty \dfrac{-x^n}{n^2} \\ &=-x-\dfrac{x^2}{4}-\dfrac{x^3}{9}-\dfrac{x^4}{16}-\cdots \end{aligned}\] To find the radius of convergence, we apply the ratio test: \[\begin{aligned} \lim_{n\to\infty}\left|\dfrac{a_{n+1}}{a_n}\right| &=\lim_{n\to\infty} \left|\dfrac{-x^{n+1}}{(n+1)^2}\cdot\dfrac{n^2}{-x^n}\right| \\ &=|x| \lt 1 \end{aligned}\] So the radius of covergence is \(R=1\).

From \[\begin{aligned} \int_0^x \dfrac{\ln(1-t)}{t}\,dt &=\sum_{n=1}^\infty \dfrac{-x^n}{n^2} \\ &=-x-\dfrac{x^2}{4}-\dfrac{x^3}{9}-\dfrac{x^4}{16}-\cdots \end{aligned}\] we get \[\begin{aligned} \int_0^{0.1} \dfrac{\ln(1-t)}{t}\,dt &=\sum_{n=1}^\infty \dfrac{-(0.1)^n}{n^2} \\ &=-(0.1)-\dfrac{(0.1)^2}{4}-\dfrac{(0.1)^3}{9}-\dfrac{(0.1)^4}{16}-\cdots \end{aligned}\] We approximate this by the first \(2\) terms: \[ \int_0^{0.1} \dfrac{\ln(1-t)}{t}\,dt \approx-(0.1)-\dfrac{(0.1)^2}{4}=-0.1025 \] Since the series is not alternating, we need to use the Taylor bound on the remainder. \[ \left|R_2f(0.1)\right| \le \dfrac{M}{3!}|0.1|^3 \qquad \text{where} \qquad M \ge |f\,^{(3)}(t)| \quad \text{on} \quad [0,0.1] \] So we need the \(3^\text{rd}\) derivative: \[\begin{aligned} f(x)&=\int_0^x \dfrac{\ln(1-t)}{t}\,dt \\ f'(x)&=\dfrac{\ln(1-x)}{x} \\ f''(x)&=\dfrac{-1}{x(1-x)}-\dfrac{\ln(1-x)}{x^2} \\ f'''(x)&=\dfrac{(1-2x)}{x^2(1-x)^2} +\dfrac{1}{x^2(1-x)}+2\dfrac{\ln(1-x)}{x^3} \end{aligned}\]

We need the maximum of \(|f\,^{(3)}(x)|\) on \([0,.1]\). So we plot \(|f\,^{(3)}(x)|\). The maximum is at \(x=0.1\).

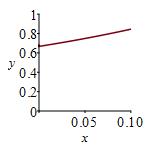
\[ M=|f\,^{(3)}(0.1)|=\dfrac{(1-2(0.1))}{(0.1)^2(1-(0.1))^2} +\dfrac{1}{(0.1)^2(1-(0.1))}+2\dfrac{\ln(1-(0.1))}{(0.1)^3} =0.844 \] Thus, \[ \left|R_2f(0.1)\right| \le \dfrac{M}{3!}|0.1|^3 =\dfrac{0.844}{6}|0.1|^3=1.4\cdot10^{-4} \]